[Paper Review] N-BEATS: Neural Basis Expansion Analysis for Interpretable Time Series Forecasting

Boris N.Oreshkin et al., N-BEATS: Neural Basis Expansion Analysis for Interpretable Time Series Forecasting, 2019

들어가며

시계열 예측에 딥러닝이 쓰이고 있긴 하지만 통계 기반 모델과 함께 쓰이는 경우가 많았다. 그러나 N-BEATS 모델은 오직 딥러닝 아키텍처로 기존 시계열 예측 컴피티션에서 통계 기반 모델과 하이브리드 모델(통계+딥러닝)의 성능을 뛰어넘는 결과를 보여주었다. 또한 해석 가능한 특징까지 가지고 있어 실무에 적용하기 적합한 모델이라고 할 수 있다. 어떤 아이디어가 숨어 있을지 살펴보자.

핵심 요약

• 딥러닝 아키텍처로 통계적 접근법을 뛰어 넘은 첫 번째 사례이다.
• 전통적인 시계열 분석 방법인 seasonality-trend level 분석법을 이 모델로 구현할 수 있어서 해석 가능하다.
• 기본적인 fully connected layer로 구성된 network가 backcast, forecast 두 개의 예측값을 내뱉고 이들이 한 블록을 이룬다. 여러 블록이 쌓여 한 stack을 구성하고 여러 stack을 쌓은 것이 모델의 최종 구조다.

문제 정의

전형적인 multi-horizon forecast 문제인데 TFT와 다르게 univariate 상황을 가정한다.

모델 구조

전체적인 구조는 아래와 같다.

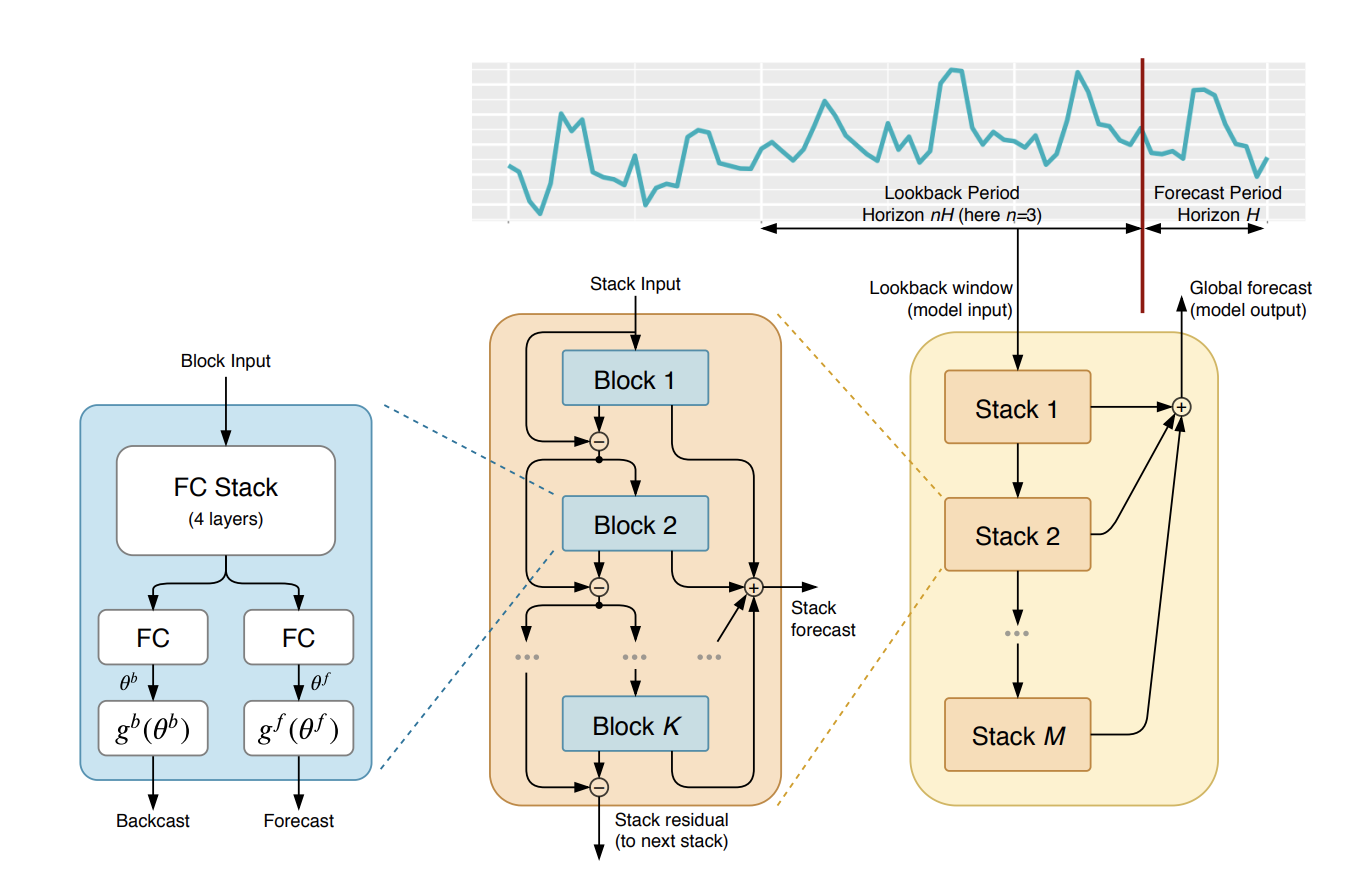
Basic block

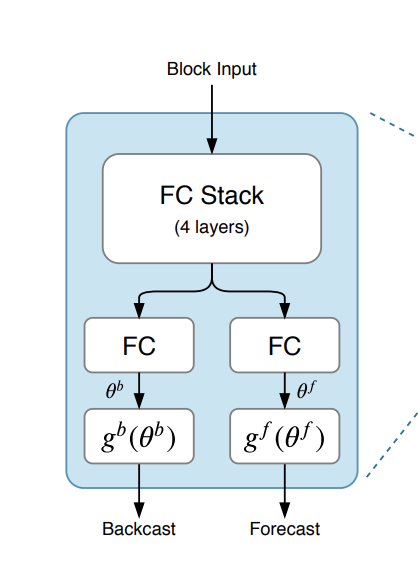
모델의 가장 작은 단위인 block은 4layers FC network와 두 갈래로 나뉜 FC layer로 구성되어 있다. 두 갈래의 FC layer는 각각 backcast와 forecast를 위한 basis expansion coefficient를 예측하도록 훈련된다.(눈치 챈 사람들도 있겠지만 이것이 N-BEATS 모델의 핵심이고 neural basis expansion이 의미하는 부분이기도 하다.) 그리고 이들이 예측한 coefficient가 basis function g에 입력으로 쓰여 한 block에서의 backcast, forecast output이 나온다. basis function g는 추후 언급할 한 stack 내에서 공유된다.

Doubly residual stacking

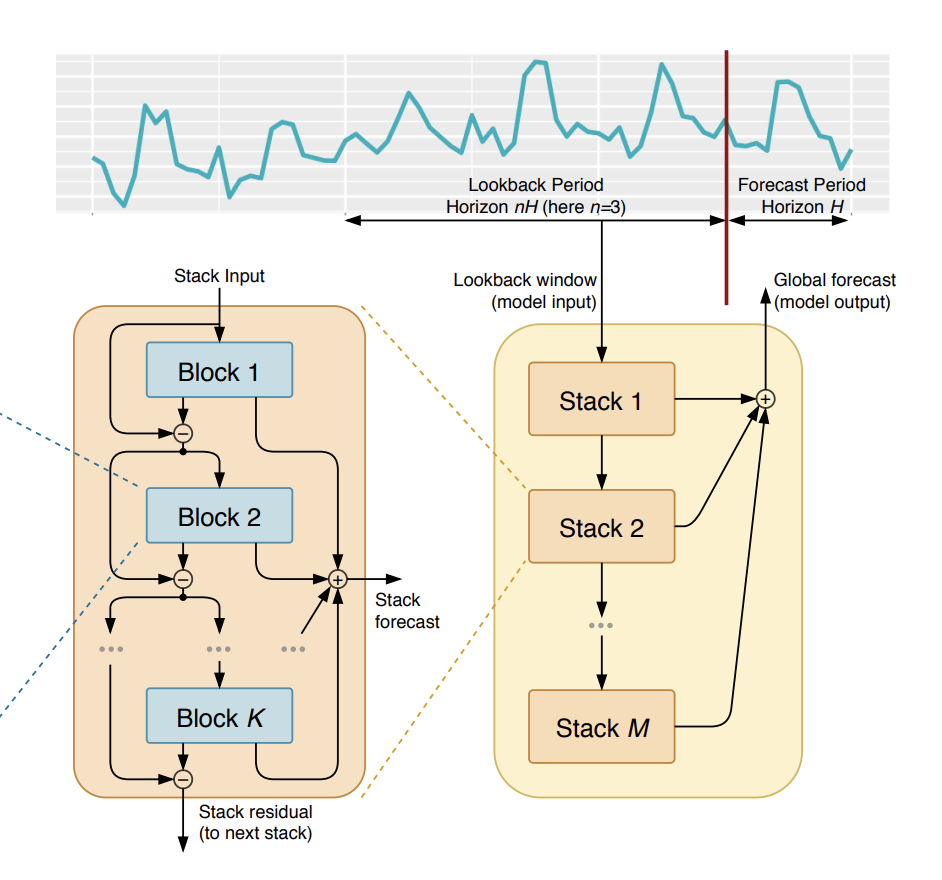
block들을 쌓는 과정에서 backcast와 forecast 예측값은 각기 다른 방식으로 stacking된다. 일종의 residual connection으로, backcast branch에서는 input signal에서 각 block의 backcast값을 빼주어 input signal의 sequential한 분석이 가능하게 하고 동시에 다음 층의 forecast를 쉽게 만들어주며, forecast branch에서는 각 block의 forecast output을 더하여 최종 forecast를 만드는데 이는 hierarchical decomposition을 하는 효과가 있다.

해석 가능성

이전까지 basis function이 임의로 정해지고 학습 가능했던 구조는 generic architecture라고 부르고, 여기에 시계열에 특화된 지식을 가미한 basis function을 정해주게 되면 interpretable architecture가 된다. 만약 basis function을 다항식으로 정한다면 이는 trend model이 되고 주기성을 가진 cos, sin 함수로 구성된 Fourier series로 정한다면 이는 seasonality model이 된다.

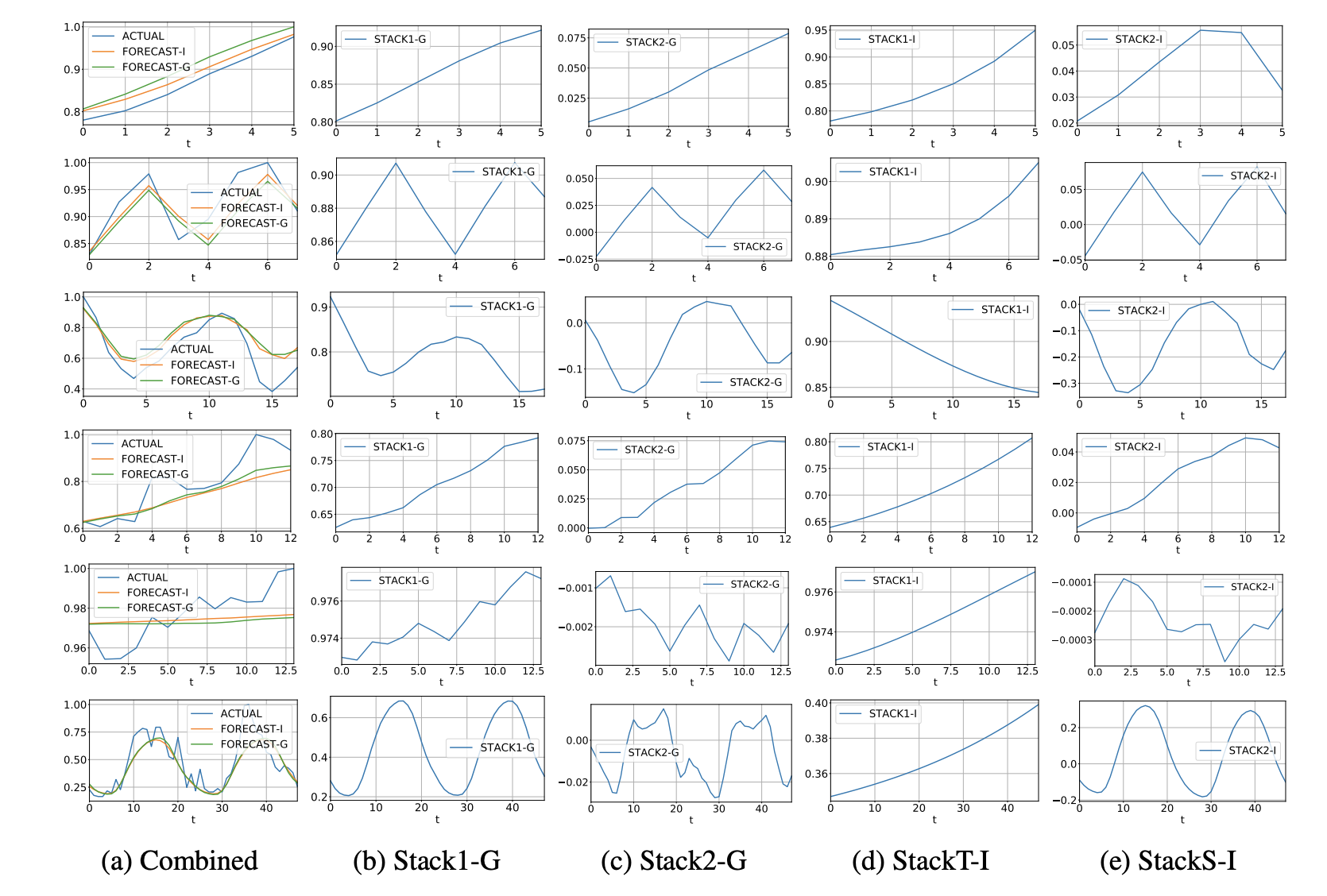
이 그림에서 각 행은 frequency별(Yearly, Quarterly, Monthly, Weekly, Daily, Hourly) 시계열 데이터 예시를 보여주며, (a)열에 있는 것이 실제 데이터이다. (a)열에 있는 FORECAST-G와 FORECAST-I는 각각 (b),(c) / (d),(e)의 stack 2개를 합친 결과로 모두 actual과 유사한 예측을 보이는 것을 알 수 있다. 따라서 trend, seasonality stack으로 구성된 interpretable 모델이 generic 모델과 비교했을 때 성능의 손실 없이 (d),(e)와 같이 interpretable한 결과를 보여줄 수 있다고 해석할 수 있다.

손실 함수

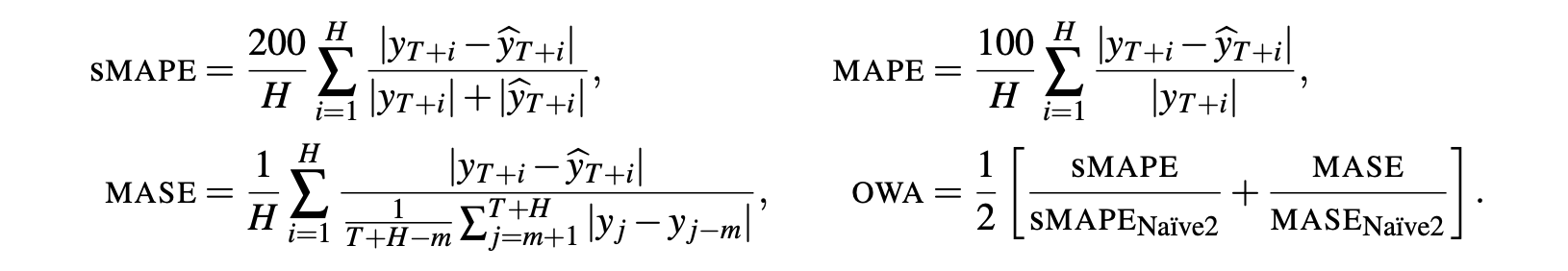
dataset에 따라 OWA, SMAPE, MAPE를 사용하였다.

예측 성능

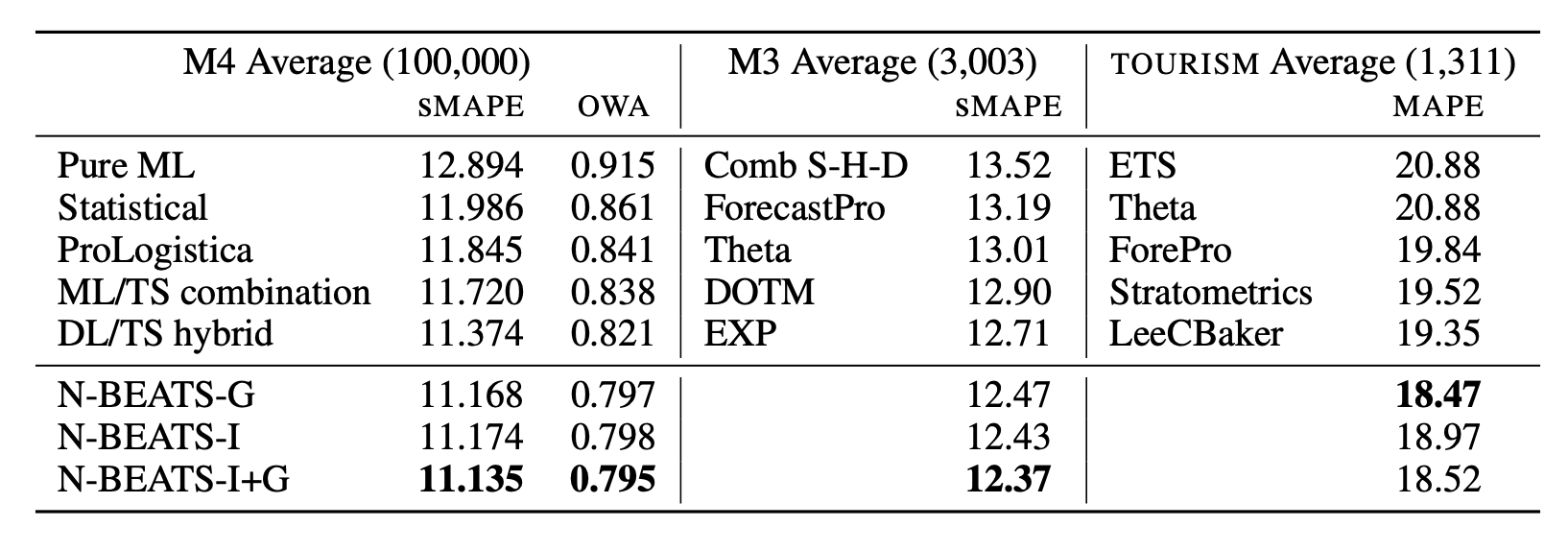
M4, M3 dataset에 대해서는 N-BEATS의 generic model과 interpretable model을 ensemble한 모델이 가장 좋은 성능을 보였고, TOURISM에서는 generic model이 최고의 성능을 나타냈다.

결론

FC layer와 ReLU만을 이용하여 SOTA 성능을 내는 시계열 예측 모델을 만들었다. CNN, RNN과 같이 복잡한 모델 구조를 사용하기보다 계층적인 학습이 가능하도록 block을 구성한 아이디어가 학습 향상에 기여한 것으로 보이며 높은 성능과 모델 구조를 유지하면서 기존의 시계열 분석에 사용되던 trend, seasonality 또한 분석할 수 있는 것이 큰 장점이다. 사전에 데이터셋과 관련된 어떠한 지식도 사용하지 않으므로 어떤 시계열 데이터든 적용가능하고 univariate 시계열 예측 문제에서는 널리 쓰일 수 있는 모델이라 생각한다.