[Paper Review] RawBoost: A Raw Data Boosting and Augmentation Method applied to Automatic Speaker Verification Anti-Spoofing

RawBoost

Tak, Hemlata, et al. “Rawboost: A raw data boosting and augmentation method applied to automatic speaker verification anti-spoofing.” ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2022.

들어가며

Raw waveform을 입력으로 받아 진위여부를 판별하는 end-to-end(E2E) 방식의 오디오 딥페이크 탐지 모델이 인기를 얻고 있다. E2E 모델을 학습할 경우, 기존에 사용하던 2차원 오디오 표현(e.g. 멜 스펙트로그램) 기반 어그멘테이션 기법들은 사용할 수 없게 된다. 본 논문에서는 이러한 단점을 해결하기 위해 raw waveform 형태 입력에 바로 적용할 수 있는 어그멘테이션 기법인 RawBoost를 제안한다. RawBoost는 noise recordings, impulse responses와 같은 추가적인 데이터가 없이도 어그멘테이션을 할 수 있다는 장점이 있다. 데이터, 어플리케이션 및 모델 등에 구애받지 않고 다양한 상황에 적용가능하며 전화 시나리오를 위해 디자인되었다.

RawBoost에서는 제안된 3가지 noise 추가 기법을 조합함으로써, 통신 환경에서 발생하는 nuisance variability를 효과적으로 모델링 할 수 있다. 여기서 nuisance variability는 모델이 예측해야 할 주요 정보와는 무관하지만, 데이터에 영향을 미치는 변동 요소를 의미하며, 이는 인코딩 방식, 전송, 마이크 및 증폭기 등다양한 요인에서 기인하는 노이즈와 선형 또는 비선형 왜곡으로 나타날 수 있다.

ASVspoof 2021 LA 데이터셋으로 평가한 결과 SOTA 베이스라인 모델에 RawBoost를 적용했을 때 min t-DCF 기준으로 27% 개선된 성능을 보였고, 외부 데이터에 의존하거나 모델 수준에서 추가적인 개입이 필요한 솔루션에만 뒤쳐진다는 것을 보여준다.

핵심 요약

• RawBoost는 raw waveform에 적용할 수 있는 어그멘테이션 기법이다.
• RawBoost는 오디오 딥페이크가 주로 사용되는 전화 시나리오를 모델링하는 방법이다.
• RawBoost는 데이터, 어플리케이션, 모델에 독립적(agnostic)이다.

제안 방법

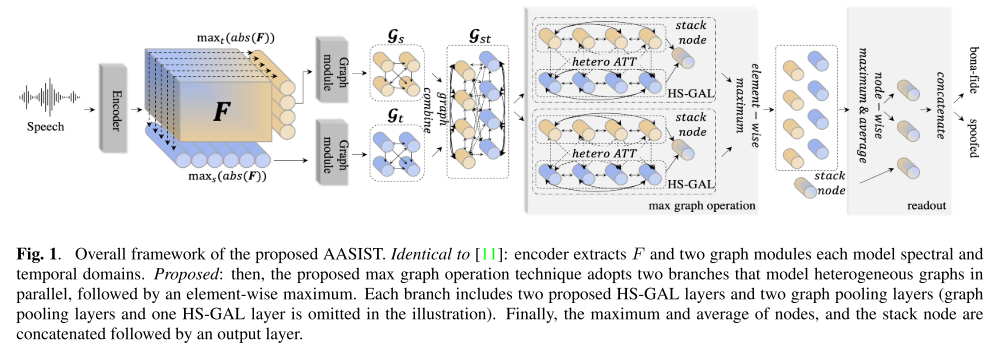
RawBoost는 선형 및 비선형 신호처리 기술을 사용하여 학습 데이터셋의 발화 집합을 증폭하거나(boost) 왜곡하고(distort), 또 추가 훈련 발화로 데이터셋을 증강(augment)시키는 역할을 한다. 이를 위해 서로 독립적인 3가지 기법을 제안하며, 각 기법의 모식도가 그림 1에 나타나 있다.

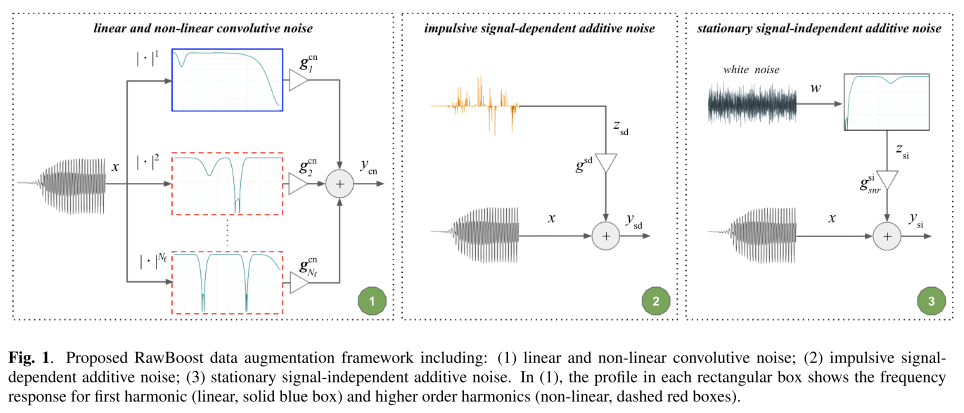
Linear and non-linear convolutive noise

먼저 첫 번째 방법은 linear and non-linear convolutive noise를 추가하는 방법이다. 어떤 채널이건 인코딩, 압축-압축해제 및 전송을 거치게 되면 stationary convolutive distortion을 만들어내고, 이러한 대부분의 채널들은 non-linear disturbance까지 만들어낸다는 사실에서 착안한 아이디어이다. 이렇게 linear 및 non-linear 왜곡에 강건한 모델을 만들기 위해서 multi-band filtering과 Hammerstein 시스템을 조합하여 사용한다.

*convolutive noise: 랜덤하게 더해지는 것이 아니라 시스템적인 방식으로 왜곡되는 noise를 말한다. 전화 통화 시 네트워크에서 특정 주파수 대역이 걸러지거나 압축하면서 원래 음성이 변형되는 경우, 마이크나 스피커에서 특정 주파수만 강조하거나 억제하는 경우 특정 필터를 통해 convolution 된 것과 같은 효과가 발생하며 이를 convolutive noise라 부른다.

• Multi-band filters

  

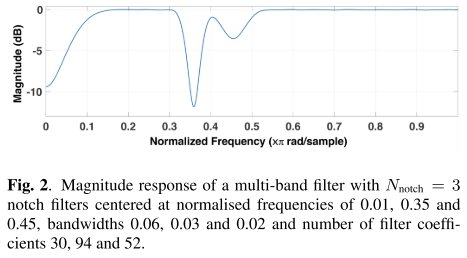
  • 시간 축으로 notch filtering을 적용해서 convolutive noise를 생성해내는 방식.
  • 여러개의 노치 필터($N_{notch}$)를 조합해서 사용한다.
  • 각 필터는 중심 주파수($f_{c}$)와 필터 폭($\Delta f$)을 랜덤하게 정해서 생성한다.
  • 각 노치 필터는 finite impulse response(FIR) 필터로 구현되며, 필터 계수 개수($N_{fir}$)도 랜덤하게 선택된다.
  • 필터 계수 수가 많을수록 더 날카로운 주파수 제어가 가능하지만 계산량이 늘어나고, 반대로 적으면 부드럽지만 패스밴드(필터가 신호를 통과시키는 주파수 대역) 리플(물결 무늬)이나 왜곡이 발생할 수 있다.
  (실습 코너) Filter 시각화하여 이해하기

  • cut_off 주파수가 3kHz인 low-pass filter
  

  
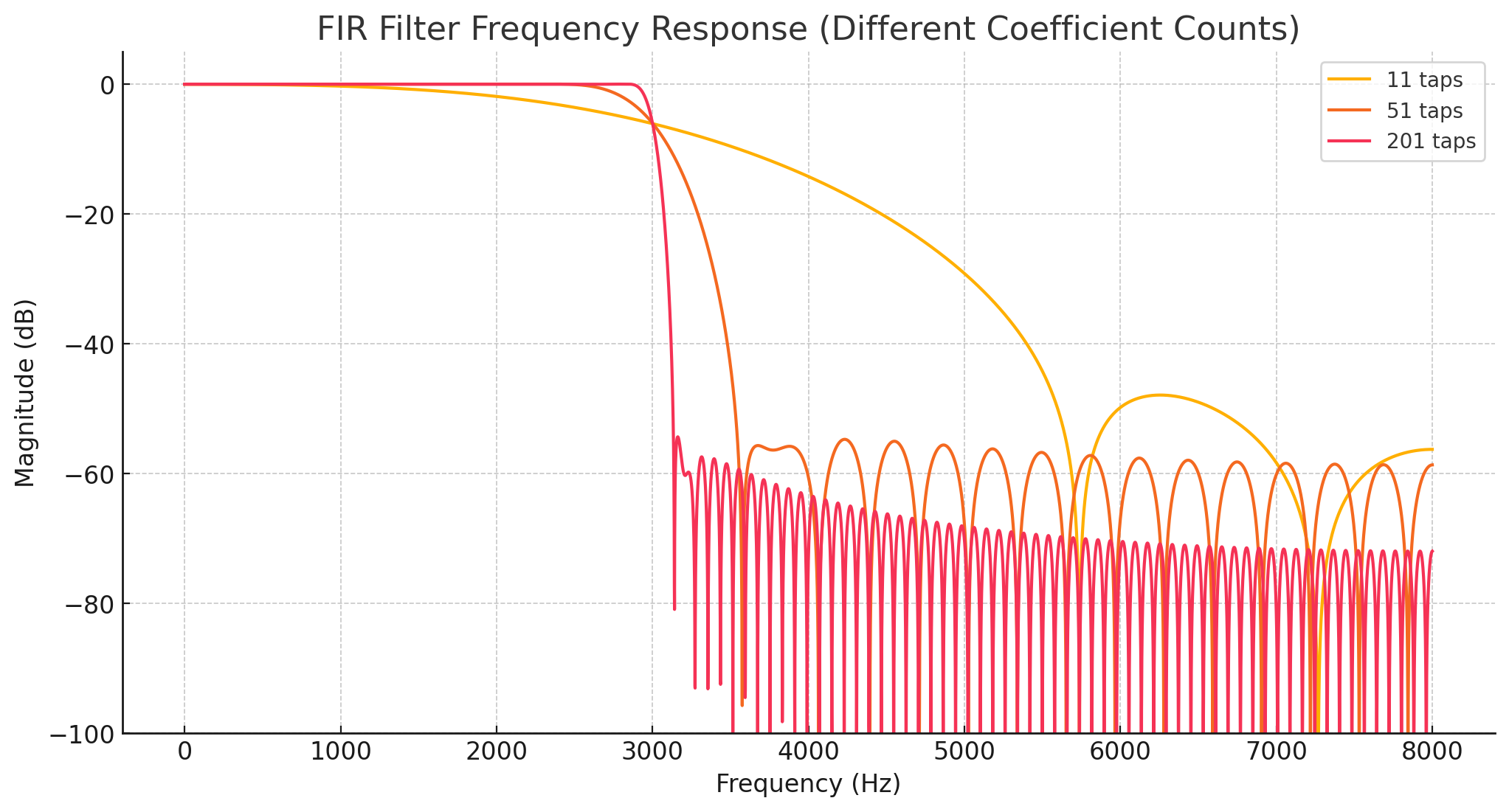
        import numpy as np
        import matplotlib.pyplot as plt
        from scipy.signal import firwin, freqz
          
        # Sampling rate and filter specs
        fs = 16000  # 16 kHz sampling rate
        cutoff = 3000  # Cutoff frequency at 3 kHz
        normalized_cutoff = cutoff / (fs / 2)  # Normalize cutoff for firwin
          
        # Different numbers of coefficients
        num_taps_list = [11, 51, 201]
          
        # Plotting
        plt.figure(figsize=(12, 6))
        for num_taps in num_taps_list:
            coeffs = firwin(num_taps, normalized_cutoff)
            w, h = freqz(coeffs, worN=8000)
            plt.plot(w * fs / (2 * np.pi), 20 * np.log10(np.abs(h)), label=f'{num_taps} taps')
          
        plt.title('FIR Filter Frequency Response (Different Coefficient Counts)')
        plt.xlabel('Frequency (Hz)')
        plt.ylabel('Magnitude (dB)')
        plt.grid(True)
        plt.legend()
        plt.ylim(-100, 5)
        plt.show()
          
        

  • 2800(cut-in) ~ 3200(cut-off) 주파수 대역을 차단하는 notch filter
  

  
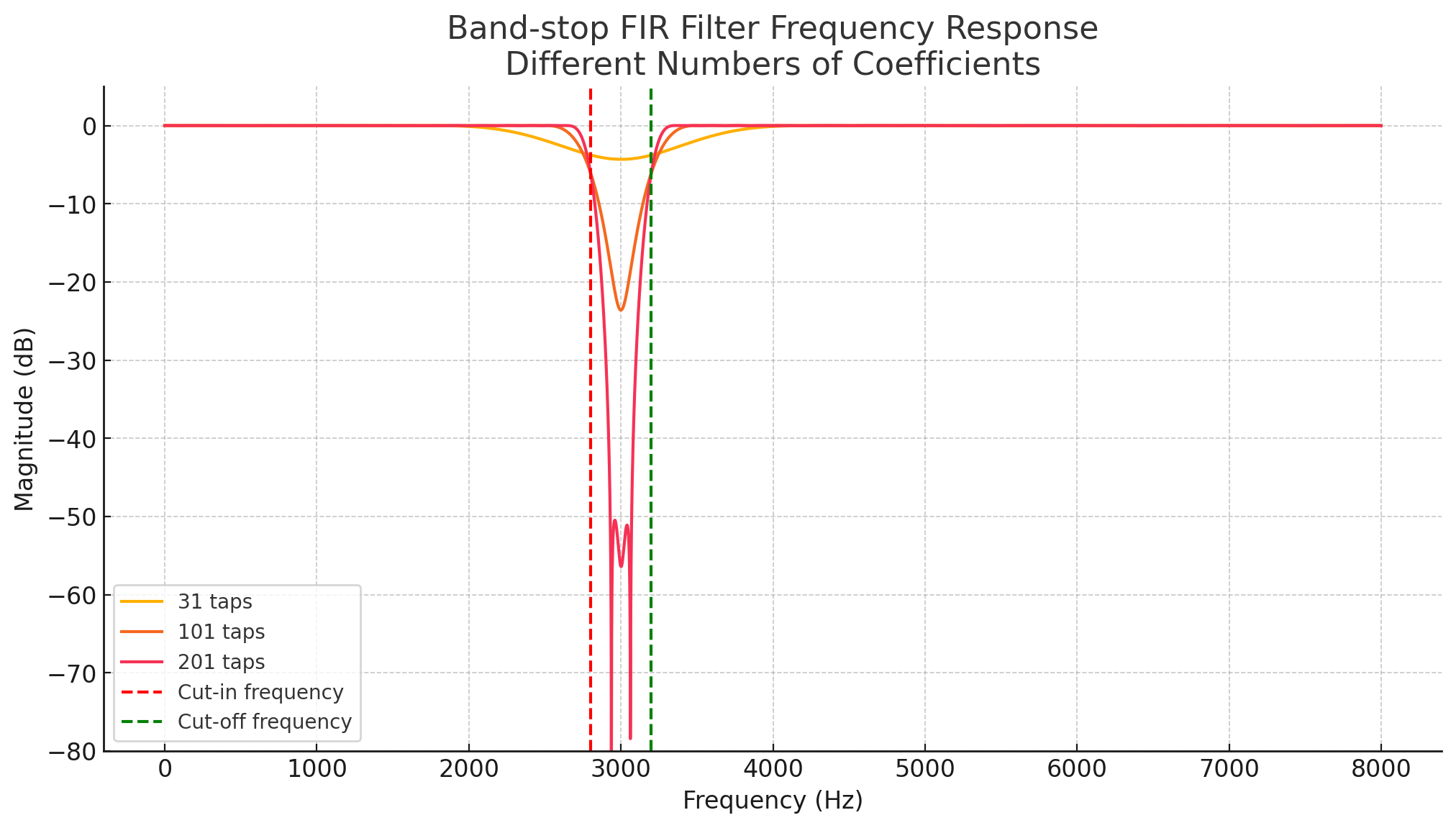
        # Define different filter lengths (number of coefficients)
        num_taps_list = [31, 101, 201]
          
        # Cut-in and cut-off frequencies (notch band)
        cut_in = 2800  # Hz
        cut_off = 3200  # Hz
        normalized_band = [cut_in / (fs / 2), cut_off / (fs / 2)]  # Normalize
          
        # Plot frequency responses for different filter lengths
        plt.figure(figsize=(12, 6))
        for num_taps in num_taps_list:
            coeffs = firwin(num_taps, normalized_band, pass_zero='bandstop')
            w, h = freqz(coeffs, worN=8000)
            plt.plot(w * fs / (2 * np.pi), 20 * np.log10(np.abs(h)), label=f'{num_taps} taps')
          
        # Add vertical lines for cut-in and cut-off
        plt.axvline(cut_in, color='r', linestyle='--', label='Cut-in frequency')
        plt.axvline(cut_off, color='g', linestyle='--', label='Cut-off frequency')
          
        # Plot settings
        plt.title('Band-stop FIR Filter Frequency Response\nDifferent Numbers of Coefficients')
        plt.xlabel('Frequency (Hz)')
        plt.ylabel('Magnitude (dB)')
        plt.grid(True)
        plt.ylim(-80, 5)
        plt.legend()
        plt.show()
  
        

• Hammerstein systems

  • 비선형 시스템 모델로, 입력에 포함된 주파수 성분 $f_0$로부터 고차 고조파(harmonics)를 생성한다.
  • 즉, $N_f - 1$ 개의 새로운 주파수 성분이 생기며, 이는 $2f_0,3f_0,…,N_ff_0$ 같은 비선형 하모닉 왜곡을 유도한다.
  • 생성되는 고조파의 주파수나 세기는 $f_0$ 성분과 비선형 시스템의 특성에 따라 결정된다.
  • 오디오 환경에서 이런 비선형 왜곡은 마이크, 스피커, 앰프 등에서 자주 발생한다.

본 논문에서 multi-band filtering과 Hammerstein 시스템을 조합하여 생성하는 convolutive noise는 아래와 같은 수식으로 표현할 수 있다.

\[y_{\text{cn}}[n] = \sum_{j=1}^{N_f} g_j^{\text{cn}} \sum_{i=0}^{N_{\text{fir}_j}} b_{ij} \cdot x^j[n - i]\]

• $x$: 원래 입력 신호 (raw waveform)
• $x^j$: j차 비선형 항
• $N_f$: 생성할 고차항의 개수 (non-linearity 차수)
• $g_j^{\text{cn}}$: j차 고조파에 대한 가중치 (랜덤값)
• $b_{ij}$: j번째 필터의 FIR 계수
• $N_{\text{fir}_j}$: j번째 필터의 계수 수
  (실습 코너) 고차항을 만들면 왜 정수배 주파수가 생기는지 이해하기

  입력 신호가 하나의 사인파라고 가정했을 때 $$ x(t) = \sin(2\pi f_0 t) $$ 제곱을 하게 되면 아래와 같다. $$ \sin^2(\theta) = \frac{1 - \cos(2\theta)}{2} $$ $$ x^2(t) = \sin^2(2\pi f_0 t) = \frac{1 - \cos(4\pi f_0 t)}{2} $$ 즉, DC 성분(0Hz)과 2차 고조파($2f_0$)가 생기게 된다. 마찬가지로 세제곱을 하면 기본 주파수 $f_0$와 $3f_0$성분이 생기고, 이를 일반화하여 n제곱을 하게 되면 그 안에는 $f_0$,$2f_0$,$3f_0$, … $nf_0$ 성분이 혼합돼 있게 된다.

Impulsive signal-dependent additive noise

두 번째 방법은 마이크, 앰프, 하드웨어 문제, 클리핑, 동기화 오류, 계산 부족 등에서 발생하는 ‘순간적(impulsive)이고 불규칙한’ 노이즈를 모델링 하고 더해주는 것이다. 이러한 노이즈는 signal-dependent하고 random noise와 같은 signal-independent 노이즈보다 크기가 작은 것이 특징이다.

본 논문에서 impulsive signal-dependent noise를 더해주는 방법은 다음과 같다.

\[y_{\text{sd}}[n] = x[n] + z_{\text{sd}}[n]\]

• $x[n]$ : 원래 입력 신호
• $z_{\text{sd}}[n]$: impulsive signal-dependent noise

즉, 전체 신호의 일부 샘플에만 노이즈를 더해준다. 그리고 노이즈를 signal dependent하게 만들기 위해 아래와 같은 방법을 사용한다.

\[z_{\text{sd}}[n] =\begin{cases}g^{\text{sd}} \cdot D_{\{-1, 1\}}[n] \cdot x[n], & \text{if } n \in \{p_1, p_2, \dots, p_P\} \\0, & \text{otherwise}\end{cases}\]

• $g^{\text{sd}}$: noise의 크기를 결정하는 스칼라 게인 값 (아주 작음)
• $D_{{-1,1}}[n]$ : 랜덤하게 -1 또는 +1을 선택 (방향만 바꿈)
• $x[n]$: 현재 신호값 → 즉, 신호 크기를 기준으로 노이즈 크기를 정함
• $p_1,…,p_P$: 전체 샘플 중 노이즈를 적용할 위치들 (무작위)

이 때, 노이즈를 적용할 위치의 수인 $P$는 다음 분포에서 샘플링된다.

\[f_R(r) =\begin{cases}- \log(r), & 0 < r \leq 1 \\- \log(-r), & -1 \leq r < 0\end{cases}\]

그리고 편의를 위해서 $P$는 오디오 전체 길이의 특정 %($P_{\text{rel}}$)로 결정하는 방식이 사용된다. 예를 들어, $P_{\text{rel}}$이 20%이고 오디오 길이가 200이라면 $P$는 40이 된다.

Stationary signal-independent additive noise

마지막 방법은 signal-independent한 노이즈를 더하는 것이다. 이러한 형태의 노이즈 사용은 데이터 증강에서 가장 널리 사용되는 형태 중 하나이며, 음성 인식, 화자 인식, 감정 인식, 오디오 위조 탐지, 스푸핑 탐지 등 다양한 분야에 적용되어 왔다.

signal-independent 노이즈는 헐겁거나 제대로 연결되지 않은 케이블, 통신 채널의 간섭, 전자기 간섭, 또는 열 잡음과 같은 원인으로 발생할 수 있다. impulsive noise와 달리, 정적인 white noise $w$는 FIR필터를 거쳐 전체 발화에 다음과 같이 더해진다.

\[y_{\text{si}}[n] = x[n] + g^{\text{si}}_{\text{snr}} \cdot z_{\text{si}}[n]\] \[g^{\text{si}}_{\text{snr}} = \frac{10^{\frac{\text{SNR}}{20}}}{\|z_{\text{si}}\|^2 \cdot \|x\|^2}\]

• $x[n]$: 원래 입력 신호
• $z_{\text{si}}[n]$: FIR 필터를 통과한 white noise
• $g_{\text{snr}}^{\text{si}}$: SNR에 기반한 스케일링 계수

실험 결과

ASVspoof 2021 챌린지 룰에 따라서 학습에는 ASVspoof 2019 LA training과 development 셋을 사용하고, 평가에는 ASVspoof 2021 LA 전체를 사용한다. 평가 지표로는 min t-DCF를 기본으로 사용하되, EER도 함께 보고한다.

베이스라인 모델로은 오픈소스로 공개된 RawNet2 모델을 사용하며, 첫 번째 sinc 레이어는 20 mel-filter bank로 초기화되었다. 그리고 각 필터는 1025 샘플(약 64ms 초)에 해당하는 impulse response를 가지며 이는 raw waveform과 컨볼루션된다. 이후 필터링된 신호는 4초(64,600 샘플) 단위가 되도록 잘리거나 결합된다. sinc 레이어 뒤에는 residual 네트워크와 GRU가 이어지며, 최종적으로 입력 오디오가 bona fide인지 spoofed인지 예측한다.

RawBoost 기법 3가지는 series로 연결해서 사용하거나, parallel하게 사용되었으며 각 기법에 쓰인 파라미터는 다음과 같다.

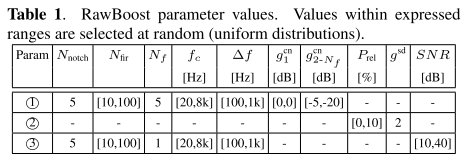
실험 결과는 다음과 같이 RawNet2 모델에 각기 다른 증강 기법을 적용하여 C1~C7 코덱 세팅에서 min t-DCF를 비교하고, pooled min t-DCF와 pooled EER도 함께 나타내었다.

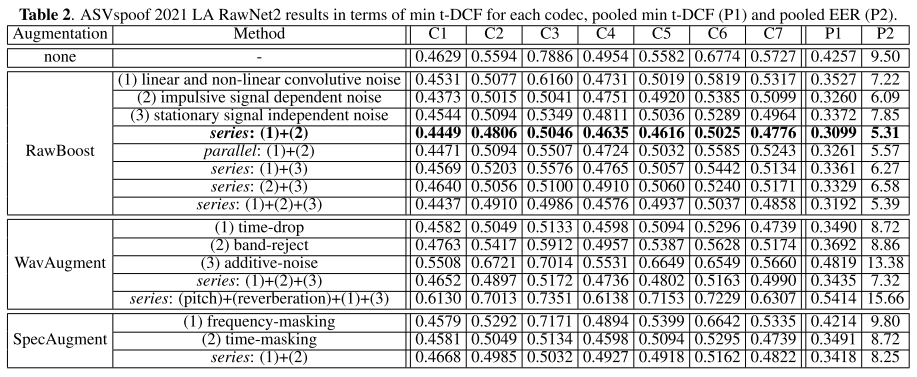
표 2에 따르면 가장 좋은 결과는 RawBoost 1,2번 기법을 series로 사용할 때 나타났으며 pooled min t-DCF 기준으로 보면 baseline 대비 27% 성능 향상이 이루어졌다. 그리고 3번 기법인 stationary noise를 더하는 방식은 단독으로 사용했을 때는 효과가 있었으나 다른 기법들과 함께 사용했을 때는 추가적인 성능 향상을 이끌어내지 못했다. 저자들은 ASVspoof LA 데이터에 주변 노이즈가 포함되어 있지 않기 때문에 이는 당연한 결과라고 말하며, PA 시나리오 데이터는 주변 노이즈를 포함하고 있기 때문에 효과가 있을 것이라고 주장한다.

더 나아가 데이터 증강기법의 효과에 초점을 맞춰 다른 시스템들과 성능을 비교해보았다.

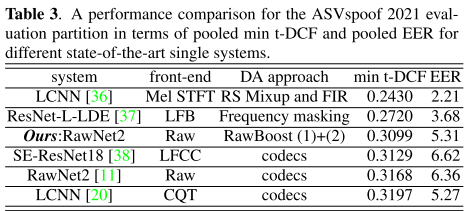
3번째로 좋은 결과를 보였는데, 상위 3개 시스템들 중 유일하게 RawNet2만 raw waveform을 입력으로 받는다. ResNet-L-LDE는 MUSAN을 외부 데이터 소스로 하여 데이터를 추가하지만, RawBoost는 추가적인 데이터가 필요없다. 그리고 LCNN은 RS mixup을 사용하는 과정에서 loss function 수정과 같은 모델 수준의 수정이 이루어지지만, RawBoost는 모델 수준의 개입이 전혀 이루어지지 않는다. 또한, 나머지 시스템들은 코덱을 데이터 증강기법으로 사용하고 있는데 RawBoost는 어떠한 코덱도 필요가 없다.

따라서 본 논문에서 제안하는 RawBoost는 외부 데이터가 필요없는 방식(data-agnostic)이고 모델 수준의 개입이 일어나지 않는 방식(model-agnostic)이며, 비슷한 nuisance variability가 존재할 것이라고 기대되는 다른 오디오 분류 태스크에도 적용될 수 있는 방식(application-agnostic)이라고 할 수 있다.

의견

• 오디오 통신 상황에서 발생할 수 있는 노이즈들을 디테일하게 구분하고 모델링 한 것이 인상적이다.
• 실제로 통신 상황의 데이터가 없는 ASVspoof 2019 데이터에 RawBoost만 적용 했을 때, 통신 상황의 데이터인 ASVspoof 2021에 robust한 결과가 나온게 저자들이 실제 상황에 가까운 노이즈를 성공적으로 모델링 해냈음을 보여준다고 생각한다.
• 이 논문을 읽으면서 신호처리에 대한 개념들을 배울 수 있어서 좋았고, 오디오 데이터를 다루는 사람들이 꼭 읽어야 하는 논문이라고 생각한다.